dB HL - Sensitivity to Sound - Clinical Audiograms
dB HL - Sensitivity to Sound - Clinical Audiograms
Clinicians measure sound intensity in dB HL (decibels Hearing Level), i.e. dB relative to the quietest sounds that a young healthy individual ought to be able to hear. In a clinical audiogram test, pure tones between ca 250 and 8000 Hz are presented at varying levels, to determine a patient's pure tone detection thresholds (the quietest audible sounds) in the left and right ear. Thresholds between -10 and +20 dB HL are considered in the normal range, while thresholds above 20 dB HL are considered diagnostic for mild, moderate, severe or profound hearing loss, as shown here:
Particular causes of hearing loss will be show up in the clinical audiogram in characteristic ways.
Conductive Hearing Loss
Conductive hearing loss comes about when the transmission of sound to the inner ear is impaired, perhaps due to impacted ear wax (cerum), an ear infection (otitis media with effusion or OME), or calcification of the middle ear ossicles (otosclerosis). Conductive hearing loss tends to a loss of sensitivity across the entire range of frequencies, most commonly in one ear only. A so called "bone conduction test", where sound is delivered as vibration to the skull rather than as airborne sound to the ear canal, can be used to confirm a suspected conductive hearing loss.
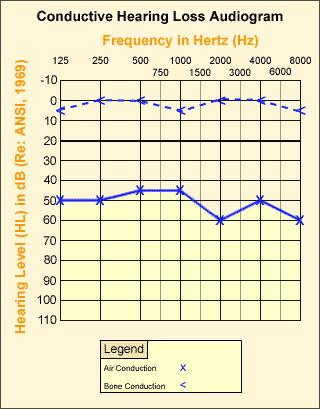
(image source: US Occupational Health Administration)
It is often possible to treat conductive hearing loss by removing the cause of the physical obstruction.
Sensory-Neural Hearing Loss
By far the most common cause of sensory neural hearing loss is damage to sensory hair cells in the cochlea. The outer hair cells in particular are very fragile, and can be damaged by exposure to excessively loud sounds, or they may simply "wear out" in old age. In rarer cases, hair cells can also be damaged by certain chemicals (such as high doses of aminoglycoside antibiotics). Sensory-neural hearing loss can also be caused by damage the auditory nerve, but conditions producing such damage are relatively rare, while noise damage or age related hearing loss are very common complaints. Central hearing loss (due to damage to the central nervous system) is rarer still. Noise damage or age related hearing loss tends to produce characteristic deficits as shown in the audiograms here below. Unlike conductive hearing loss, which can often be cured, sensory-neural hearing loss is in most cases irreparable, and treatment will aim to make the best use of those auditory structures that remain in tact, perhaps by boosting sensitivity through a hearing aid, or, in severe cases, by trying to bypass dead sensory hair cells with cochlear or brainstem implants.
Noise damage
Because our outer and middle ear transmits frequencies near 4 kHz very efficiently, hair cells that are tuned to frequencies near 4 kHz are particularly vulnerable to noise damage. Therefore, audiograms of patients with noise damage often have characteristic 4 kHz notches, as shown here:
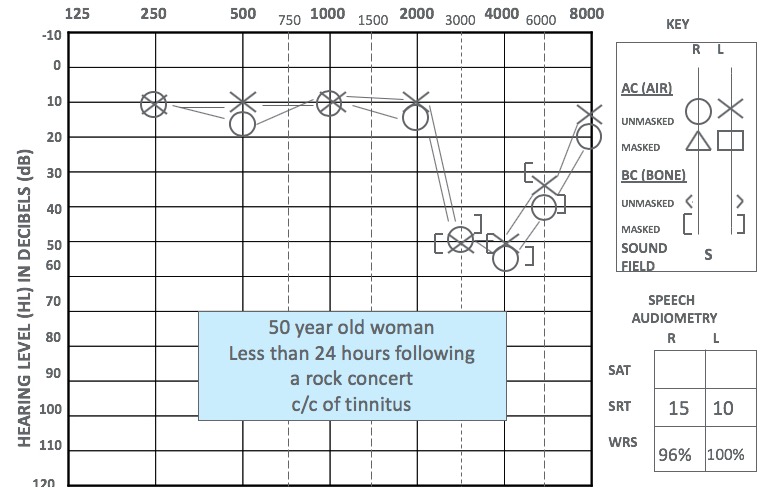
(image source: audiologyonline.com)
Age-related Hearing Loss (Presbycusis)
Even if we avoid exposure to very loud noise, the ear's outer hair cells may also simply wear out as we age, leading to age related hearing loss. In this condition, high frequency outer hair cells tend to die off before low-frequency ones, possibly because the high frequency outer hair cells have to work harder if their job is to amplify acoustic vibrations on a cycle by cycle basis. Consequently, patients with age-related hearing loss often have normal sensitivity at low frequencies, but progressively poorer sensitivity for higher frequencies, as shown here:
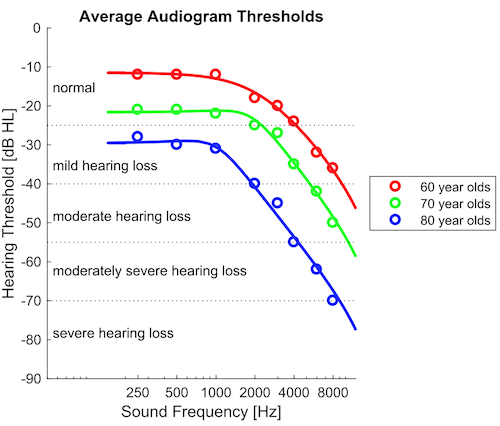
If you are curious about what the effect of such age related hearing loss would be, try our Age Related Hearing Loss Simulator.