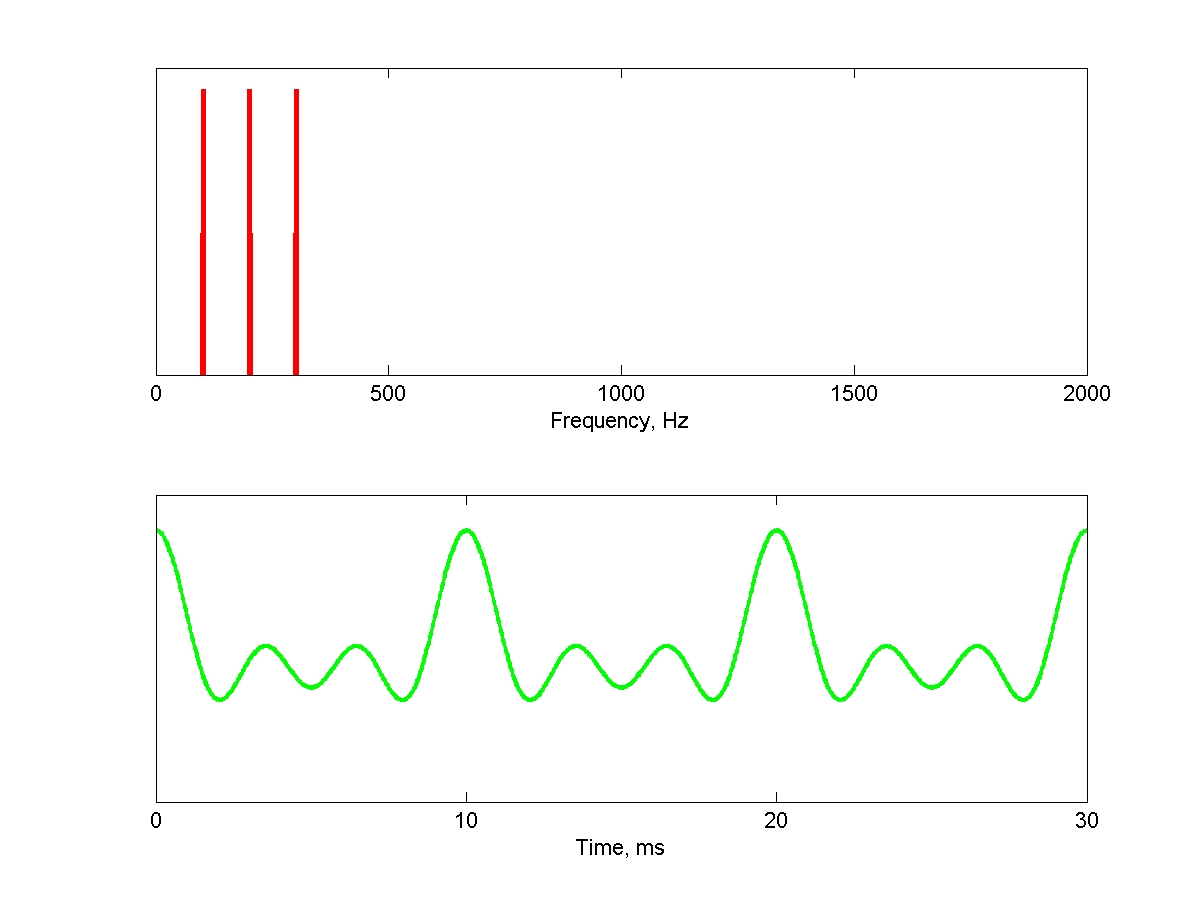
Harmonic complexes composed of 3 consecutive harmonics are among the simplest periodic sounds. Their periodicity is determined by the spacing between the harmonics. Here is such a complex, composed of harmonics 1 (the fundamental), 2 and 3 of 100 Hz. The top panel shows the spectrum of this sound, and the bottom panel shows a 30 ms long segment of the waveform, consisting of three periods (100 Hz corresponds to a period of 10 ms). The pitch of this sound is very obvious:
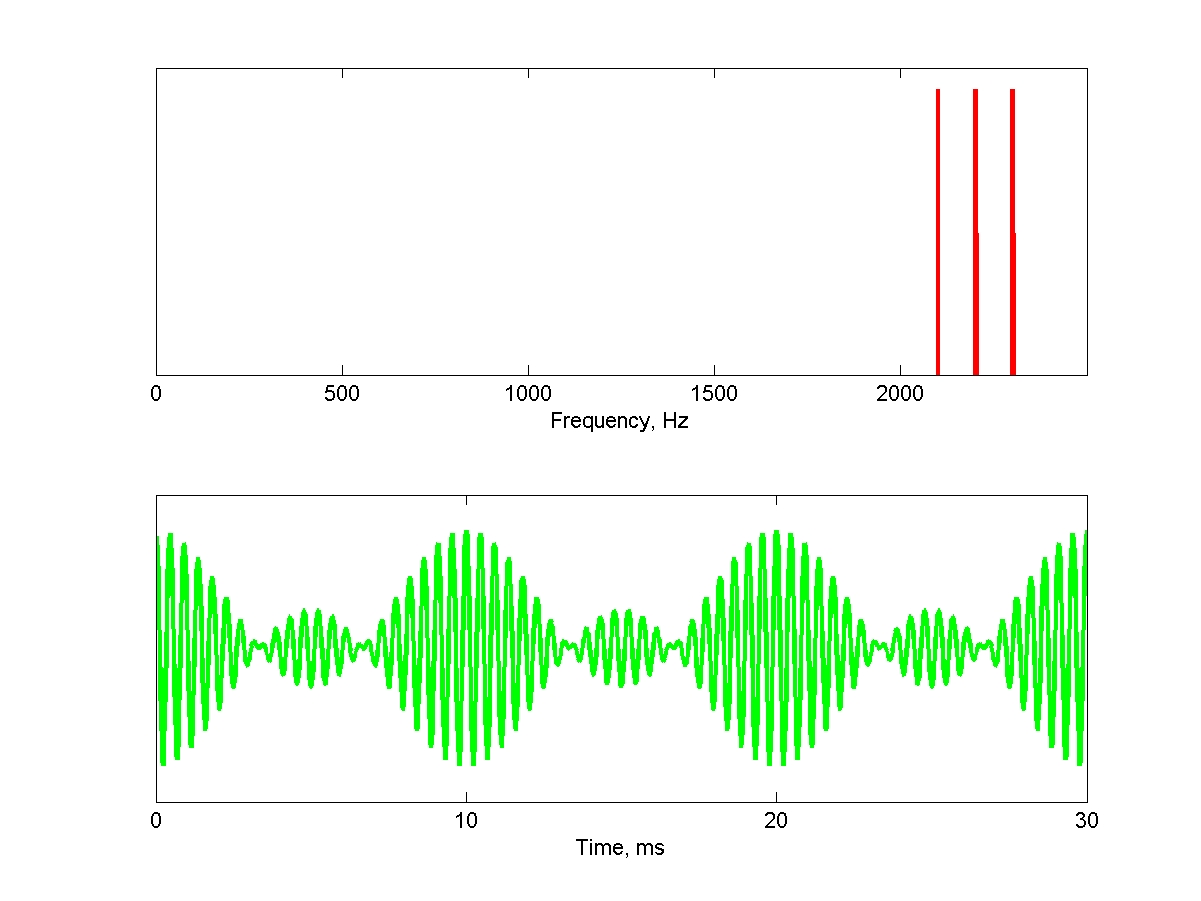
These complexes, when built of harmonics of very high harmonic number, still have the same periodicity. However, their pitch is not at their periodicity anymore. Here is a complex composed of harmonics 21, 22 and 23 of 100 Hz (note: you should lower the volume of the computer loudspeakers to avoid generating harmonic distortions that would regenerate the fundamental!):
How high can the harmonic numbers of the components be for a periodicity pitch to appear? Note that this demonstration stretches the capabilities of poor-quality computer speakers. These have hard time reproducing sounds with frequencies below a few hundreds Hz, but generate serious harmonic distortions at frequencies of a few thousands Hz. Thus, to hear the examples with low harmonic numbers you will need to use a high sound volume, while to avoid regenerating the fundamental by harmonic distortions in the examples with high harmonic numbers you will need to use low sound volume.
Harmonics 1 to 3
Harmonics 2 to 4
Harmonics 3 to 5
Harmonics 4 to 6
Harmonics 5 to 7
Harmonics 7 to 9
Harmonics 9 to 11
Harmonics 11 to 13
Harmonics 13 to 15
Harmonics 17 to 19
Harmonics 21 to 23