The following demo explores the effect of temporal regularity, or rhythmicity, on stream segregation. It uses the stimuli used in the study by Rajendran and colleagues (2013 JASA-EL).
This demo works well with recent versions of Google Chrome, Firefox and Safari.
Rapidly alternating (ABAB...) tones are usually perceived, at least initially, as a single "trill"-like sound, but after a while the single auditory stream may appear to break into two, with either the A-A- or the -B-B sequence dominating the percept, and the other tone sequence becoming a "background" sound. The wider the frequency separation, the quicker generally the break-up into two streams. Here are two example ABAB sequences with frequency separations of either 1 semitone (heard by most as one stream throughout) or 10 semitones (heard by most as two streams after only a second or so).
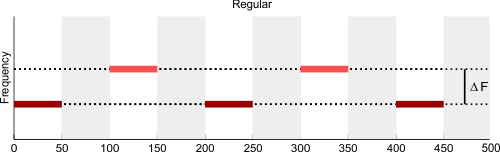
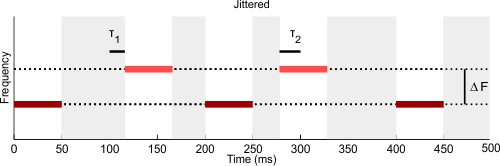
Wider frequency separation is not the only factor that increases the likelihood that two streams are perceived instead of one. Another factor which seems to play a role is temporal irregularity. Here you can try 3 second long sequences of varying frequency separation, and you can also introduce varying degrees of temporal irregularity ("jitter") into the higher frequency tone sequence.