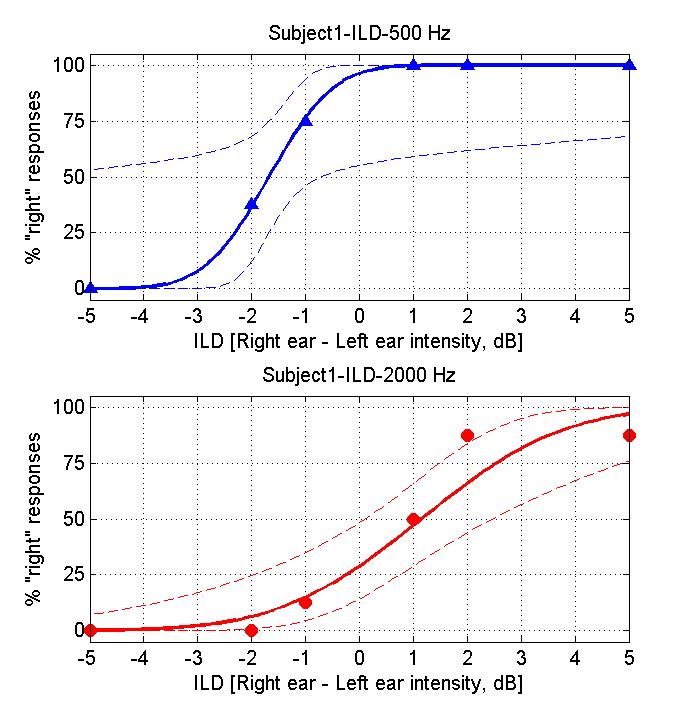
当你完成试验后,程序将为你生成一个结果图,它看起来应该差不多是这样的:
如果做这些试验是属于教学课程的一部分,你应该考虑打印这些结果图表,以便在必要时向你的老师展示(图表左上方应该有一个"File | Print"菜单)。
图中的三角形或圆形符号表示你对x轴给定的ILD值响应为“右侧”的频率。实线连线是软件根据你的结果数据所拟合的"高斯累积"S型曲线。像这样的拟合曲线是通过获得的数据样本来估计出"潜在心理测量函数(underlying psychometric function)"(即描述你对特定感官参数变化的敏感性的函数)的好方法。
问题: 在你获得的心理测量函数中,哪些ILD值与50%的“右侧”响应相关联?你预计哪个ILD值与50%“右侧”响应相关联?
心理测量曲线有助于确定你对ILD的敏感性。S型曲线的斜率越陡,需要产生“可察觉”差异的 ILD 变化就越小,即% right的变化越小。然而,人们很少用斜率值(%right/dB)来报告感觉表现。相反,他们倾向于报告“阈值(thresholds)”,即将%Right 判断从50%(完全随机猜测)提高到某个“阈值性能水平”所需的ILD变化。
练习: 选择一个阈值水平(75%的正确率可能是一个不错的选择),并确定两个测试频率的相应ILD阈值。记下这些ILD阈值。
两个频率的阈值可能非常相似或稍有不同。你能感觉到它们是否具有“有意义的差别”吗?这个问题实际上有两个部分:1)差异是否“实质性”(在生理上显著),2)差异是否可能在统计上具有显著性?对于第一部分,没有通用的标准来确定何为差异显著,你需要根据自己的判断进行评估。但是,如果差异在统计上不显著,那么观察到的两个频率的阈值差异可能并不真实。
然而,要对这个问题的第二部分做出严谨地回答,需要进行适当的统计分析,例如某种类型的bootstrap检验。这种统计技术在某种程度上超出了本实践的范围。然而,如果你以以下方式思考这个问题,你可能会对此有一些直觉:你的“真实”心理测量函数将指定每个特定的ILD下你会报告声音来自右侧的概率。但是实验无法直接测量这个概率,只能根据在有限试次的试验中实际的右侧响应频率来估计它(这里每个ILD测试了约8次)。假设某个特定ILD的真实潜在概率是75%。那么测试该ILD有点像投掷一个有75%的概率在试验中“正面”朝上的有偏硬币。在仅有8次试验的短时间内,这样的有偏硬币可能只会产生50%的“正面”朝上结果。如果你仔细思考,你可能会意识到在这个非常短的实验中观察到的右侧响应频率只是对你真实心理测量函数的非常粗略的估计。你可能还好奇图上的虚线曲线代表什么,这些是拟合到你结果数据的心理测量函数的95%置信区间。拟合S型曲线的算法会意识到它所生成的S型曲线只是一个估计,而真实的潜在函数可能与该“最佳估计”相当不同。因此,当比较两个不同频率下获得的数据时,你可以自问上图中的数据点是否来自下图绘制的置信区间,或反之亦然。
问题:在这两个测试频率下,你认为你对ILD的敏感性是基本相似的,还是存在实质性差异?