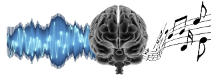
周期声音(具有重复"动机"的波形,如上图所示的蓝色曲线)的傅里叶谱必定完全由声音的"谐波"组成。谐波是周期为某个基本周期的整数倍的正弦波。上图中的红线是蓝线的"余弦相位"谐波。在考虑傅里叶谱时,我们想象蓝线由许多像红线和绿线这样的正弦波之和组成,其中我们可以根据需要调整正弦波的相位和振幅。需要注意的重要一点是,无论我们如何调整绿线的相位和振幅,它都无法成为组成蓝线所需的混合物的一部分。原因是:比较波形在周期内相同点的值,例如通过比较由点线标记的点的值。红线每个周期总是在相同的位置贡献相同的值(例如,在由灰线标记的周期上总是达到最大值)。相反,绿线无法将整数个周期"适应"到基本周期内,因此它对波的每个周期的贡献将不同,这将破坏波的周期性。因此,绿线不能是周期蓝色声波的傅里叶分量。任何其他具有周期不是声音基本周期的谐波的正弦波也不能成为其傅里叶分量。